Theoretical - Approximating Pi
The number π (pi) is a mathematical constant defined as the ratio of a circle’s circumference to its diameter. This magical number appears in many formulas in all areas of mathematics and physics.
Interestingly, pi is an irrational number, there can be no “final” digit of pi, because it’s an irrational number that never ends. It has infinite digits and it keeps ongoing, forever, without ever repeating. Which means that its value cannot be expressed exactly as a simple fraction.
Since computers can’t work with infinite decimals, they need to approximate pi. There are countless number of numerical methods to calculate the value of pi.
Practical - Approximating Pi
Write a program which approximates the value of π
There are a couple different ways of estimating π. I will use Monte Carlo Method with C programming.
What if we randomly throw darts at a dart board that looks like this.
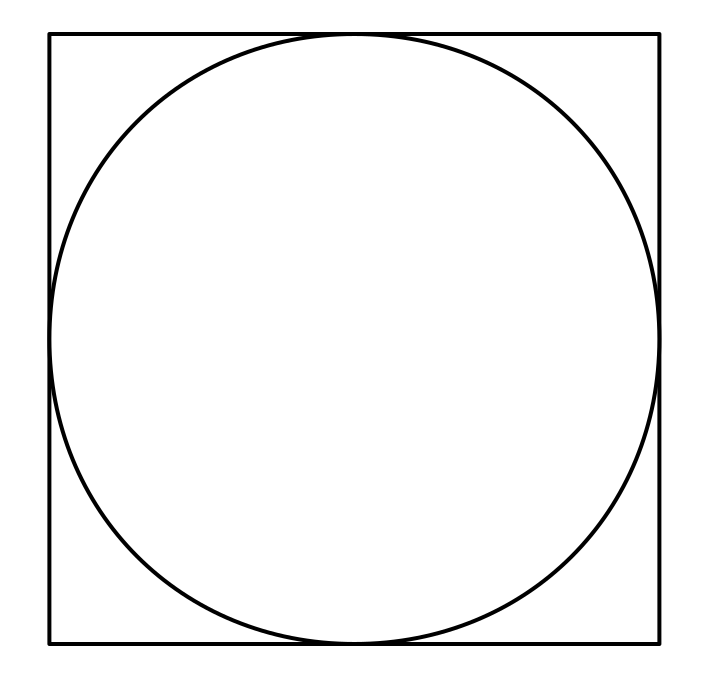
If we count up the darts that landed within the circle and compare to the total number of darts thrown, the ratio should approximate to the area of the circle divided by the area of the square.
From the figure, it’s clear that the length of the square L is twice the radius of the circle r. So we can calculate the ratio between the areas of circle and square as following.
<table cellspacing=0 border=0 align=center>
</table>
So if we randomly throw the darts, the ratio should approximate to π/4. Therefore we can just multiply the ratio by 4 to get an estimate for π.
First, we need to include math.h library to our program. Then imagine a 500x500 square and a circle which perfectly fits inside of it. I will take the center of the circle as origin point (0,0).
To be more precise I want to use float values instead of integers. rand() function returns a random integer in the range of 0 to RAND_MAX. RAND_MAX is a constant whose default value may vary between computers.
After generating 2 random float numbers between -500 and +500 as a (x,y) point in space we should calculate its distance from origin. If distance is smaller than radius of the circle (500), this means dart landed within the circle.
If we continue this process, 4 x ratio of darts inside the circle to total thrown darts will come out to π.
- C programming
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
int main()
{
float x, y, distance, approx_pi, total_count = 0.0, circle_count = 0.0, real_pi = 3.141592;
while(1) // Loop
{
// Generate two random float number.
x = (float)rand() / (float)(RAND_MAX / 1000) - 500.0;
y = (float)rand() / (float)(RAND_MAX / 1000) - 500.0;
total_count++; // Throw a dart
distance = sqrt(pow(x, 2) + pow(y, 2)); // Calculate the distance to origin
if(distance < 500.5) circle_count++; // Dart is inside the circle
approx_pi = 4.0 * circle_count / total_count; // Calculate pi
if(fabs(approx_pi - real_pi) <= 0.000001) // If we close enough
{
printf("Success: %f\n", approx_pi); // Print best approximation of pi
break; // Stop the loop
}
else printf("%f\n", approx_pi); // Print estimated pi
}
return 0;
}
- Python Programming
def distance(x, y):
return ((250-x)**2 + (250-y)**2)**0.5
while(True):
x, y = random.randint(0, 500), random.randint(0, 500)
total += 1
if distance(x, y) < 250.5:
inside += 1
pi = 4.0 * inside / total
print(pi)
Simulation: code is here.

Here is a great visual explanation of what we tried to do using Javascript. Also in this video Processing (Java) used.